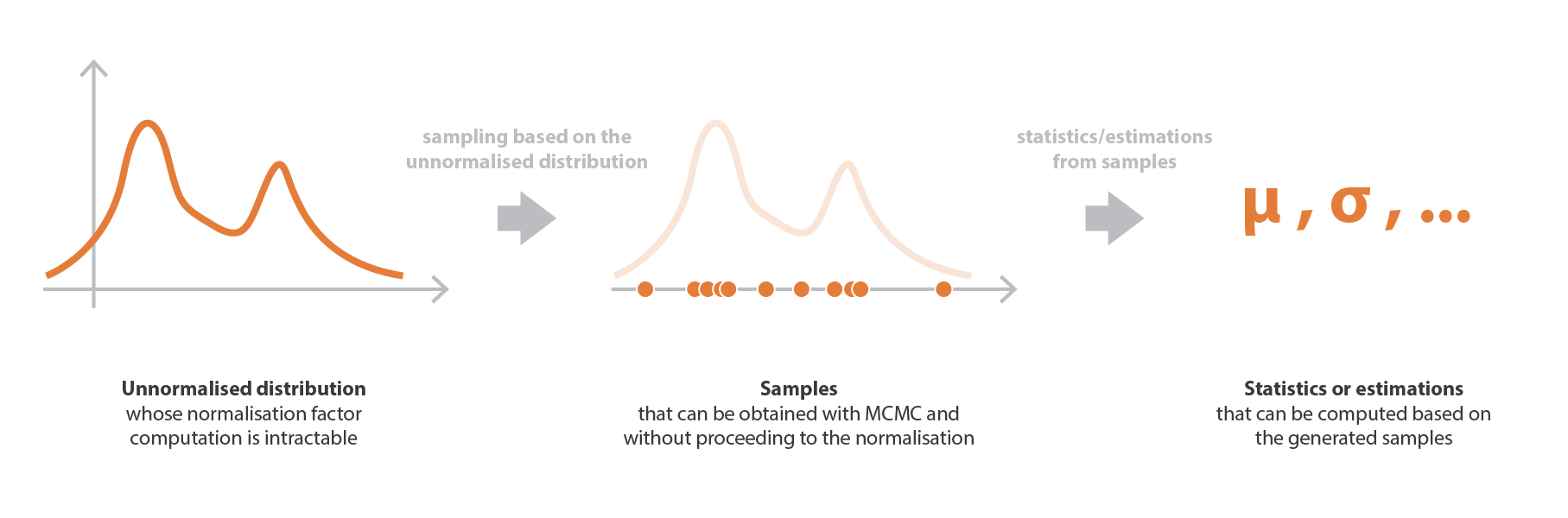
We are given an arbitrary function f and we want to draw samples from this function. Why?
For example, because we are interested in the mean and standard deviation of this function so we can summarize it with these values.
It is not important where this function comes from.
Maybe you guessed its form based on some observations or you have combined several standard functions to a more complex function that is not so easy anymore.
How can you draw samples from this arbitrary function?
The main idea of the Metropolis–Hastings algorithm is to start with a random value (input, x-value) and in each step decide whether to stay at this value or move on to some value in the near neighborhood (left or reight).
The clue is that you move to the neighborhood with a probability that is identical to the probability of this neighborhood.
For example, if you are currently on a value that has a probability of 0.2, but the point next to you has a probability of 0.25, you will, on average, end more often at the point next to you than at the point you are currently at.
How can you calculate the probability? You calculate the function's value at this point!
(To fully understand this you have to think about the function f as a density function, so the area under f can be interpreted as the mass of the function that is concentrated at this point)
If we now look for another candidate (the point next to us), we can calculate the candidate's function's value.
If the candidate turns out to have indeed a higher function's value, which also means higher probability, we move on to the candidate because it's more promising.
If we repeat this process a long time, we obtain a long list of samples or input values.
And the more probable inputs will occur more often because the algorithm is designed in such a way that each value occurs approximately as often as its probability value.
If we calculate the histogram for this list of samples, the shape of the histogram will roughly resemble the real function's shape.
Thus, we have found a way to get close to the function without actually ever writing down its true form.
You can read more about the algorithm's intuition at Wikipedia.